A new twist on the fraction-competent problem

On Sunday I attempted to measure what fraction of the cells in some cultures were competent (able to take up DNA fragments and recombine them into their chromosome).  I've previously written about this kind of analysis here and here.

Usually when I do this kind of experiment I find that only some cells were competent (anywhere from about 10% to about 50%).  But this time I got a very different result, and I don't know why.

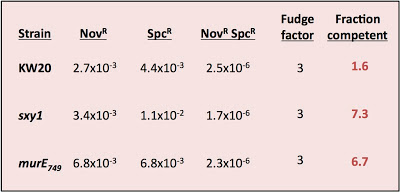
I was testing three strains - wildtype cells (strain KW20) and two hypercompetent mutant derivatives, carrying the sxy1 and murE749 mutations.  Both KW20 and sxy1 have been tested several times before; mutrE749 hasn't.

The procedure is simple.  Transform cells with MAP7 chromosomal DNA and select for two antibiotic resistance mutations located far apart on the chromosome (so they won't ever be carried on the same DNA fragment).  Select for each resistance separately and for the two together (double-transformants).  Count the resulting colonies and calculate the transformation frequency for each resistance separately and for the double-transformants.

Calculate the fraction competent as the product of the two single-mutation transformation frequencies divided by the double-transformant frequency and by a fudge factor somewhere between 2 and 4.

The fudge factor incorporates two sub-factors accounting for different effects.  The first effect is the chance that a single cell took up and recombined two DNA fragments, each containing one of the mutations, but that the incoming DNAs recombined with different strands so that, when the cell divided, one daughter cell got one mutation and the other got the other.  This factor is complicated by the unknown effects of mismatch repair, but on average 2 is the appropriate value. The second effect is whether the cells did any cell divisions before they were placed on the agar to grow into colonies.  If they did, then cells transformed by a single mutation will have given rise to one resistant colony and one sensitive colony.  This factor should  have a value of 2 if all the cells had time to divide before plating (if, for example, they needed time to express the antibiotic resistance), by less than 2 if only some did, and by 1 if the cells were plated immediately after transformation.  In my experiment I didn't allow any expression time* so this second factor should be closer to 1 than 2.  For simplicity I'll use a complete fudge factor of 3.

* In retrospect I should have allowed expression time, because one of the markers I was selecting for is spectinomycin resistance, which we think of as needing an hour's expression time.  But I forgot and, rather surprisingly, still got tons of transformants.

Here are the calculations:

What's wrong with these nice numbers?  The fraction competent should ALWAYS be less than 1; that's why it's called a fraction!

Might my assumptions be invalid?  This analysis requires that cells be able to take up more than one fragment of DNA, and that taking up one fragment does not affect the probability of taking up another fragment.  Because previous experiments have always given values less than 1, we've been assuming that this requirement is met.  But this new result only makes sense if many of the cells could only take up one fragment of DNA.

Might my DNA or plates be faulty?  The problem isn't due to using some new DNA prep with different properties; I used a fresh tube of the same MAP7 DNA stock we've been using for years.  Could it be because I forgot to give the cells some expression time after DNA uptake?  Might the lack of expression time reduced the numbers of double transformants (SpcR NovR) much more than it reduced the numbers of single SpcR transformants?  But lack of expression time doesn't appear to have been a problem, since I got at least as many SpcR transformants as NovR transformants.  The DNase I stock could be a problem.  The transformation reactions are stopped after 15 minutes by adding DNase I to degrade the remaining DNA - a few days ago I tested the DNase I stock, by adding it to the DNA 5 minutes before I added the cells, and found that it wasn't very effective - the residual transformation frequency was still quite high.  This means that some cells might have taken up DNA while they were on the plate, but since this would only exacerbate the expression-time problem it shouldn't have been a big factor.

I only did this experiment because it would help us interpret the lack of effect of the HI0659 knockout on growth rates (in the experiment I described yesterday).  If most cells weren't competent even in the hypercompetence mutants, then not seeing a growth defect in the culture doesn't meen that the competent cells didn't experience a growth defect.  But this weird result means I need to do more experiments to figure out the reason for the discrepancy with previous results.