As I discussed at the end of Representation matters, our present understanding of the USS-like repeats comes from analyses that were intrinsically biased. For example, the analyses presented in our USS-2006 manuscript (see link in sidebar) began with the assumption that the USS would be best defined by a unbroken string of approximately 9 bases. However some of these analyses led to consensus sequences where the flanking AT-rich segments had nearly as strong a consensus as the core we were searching for, leading me to suspect that, if we had instead searched for the flanking consensus, we might have gotten a different but equally valid (or equally invalid) USS consensus. (I'm not happy with this description of the problem, but I'll continue anyway.)
So my goal is to use a motif-search program to search the genome for highly-repeated patterns, starting the searches with as few assumptions as possible, and varying those assumptions to include other possibilities. Several such programs are available on-line; one of the grad students has quite a bit of experience with them. Usually you can just paste the sequences you want analyzed into a web form, click a few boxes, and the analysis appears on the screen (or is sent to your in-box). My kind of bioinformatics.
The grad student advises using the Gibbs Motif Sampler, which is available in simplified form through RSA-Tools and in more sophisticated form through the Wadsworth Institute. The FASTA problem is solved (thanks to helpful readers), so I first tried just giving both versions the first 25000bp of the genome sequence, in five 5000bp sequences, and asking them to find one 9bp motif. The Gibbs analysis is built on Bayesian probabilities, so it asks you to specify a 'prior' expected number of occurrences of the motif. (I'm glad that I now understand a bit about what Bayesian means, if not how to do it - see posts early this month.)
The results come back in various forms; tables of frequencies of each base at each position, and an alignment of the occurrences of the motif it found. The best way to visualize the results is to hand then alignment over to the sequence logo program Weblogo (see Representation matters).

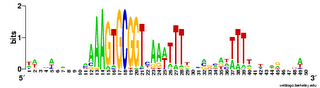
Here are a couple of examples of the logos. The one on the left comes from a search for a 10bp motif, and the one on the right from a search for a 30bp motif.
The first thing I learned (of course) was that this analysis wasn't going to be as simple as I'd hoped.
I already know that the long version of the USS consensus is a bit 'palindromic', because Ham Smith pointed this out when he discovered the long version in 1995. ...Brief interruption while I looked for a decent explanation of 'DNA palindrome' on-line, found nothing, and then drew the accompanying illustration. These base-paired DNA sequences are palindromic. In each, the sequence of the upper strand, read from its 5' end to its 3' end (red arrows) is the same as the
 sequence of the lower strand, read from its 5' end to its 3' end (blue arrows). (The analogy is to a text palindrome like "Madam, I'm Adam".
sequence of the lower strand, read from its 5' end to its 3' end (blue arrows). (The analogy is to a text palindrome like "Madam, I'm Adam".The USS consensus is far from being a perfect palindrome, but looking at the logo of the long version above shows that there are AAAs at the left end, TTTs at the right end, and a TTTAAA bit in the middle. For the Gibbs motif searches, this is enough that, if the expected number of occurrences is high (i.e. the search stringency is low), it aligns "+"-orientation USSs to "-"-orientation ones.
This only makes sense when we remember that the USS core is not at all palindromic, so on one strand it reads 5'-AAGTGCGGT and on the other strand it reads 5'-TTCACGCCA. About half the USSs in the genome point in one direction (e.g. clockwise around the genome, we can call this "+") and the other half point the other way ("-").
The tendency of Gibbs to align some of them back-to-front can be reduced (maybe even eliminated) by setting the expected number of occurrences quite low (no higher than the number of perfect USS cores we would really expect). This doesn't prevent the Gibbs program from finding more than this number. I need to think more about whether this does prevent it from finding occurrences that match quite imperfectly - my difficulty is that my own brain has a strong tendency to think mainly about the USS core.
I think this is how science is supposed to work - a kind of dialectic between reality and our biases. We start each analysis with expectations that don't match reality, then our biased analysis produces results that, although still wrong, are nevertheless closer to reality than the expectations we started with. We then take these modified expectations into the next analysis, and again get results that are a bit closer to reality. We never perfectly comprehend reality, but with good science we get closer and closer.
















I am interested to hear the details of the analyses you're doing.....like what different size motifs you are looking for (you mentioned 10-bp and 30bp in the blog) and what sort of numbers you get out at the end.
ReplyDeleteHelpful post.
ReplyDelete